↓問題のページ↓
※特に断らない限り、0-indexedを前提に記載する。
なんとか本番ACには成功したが、超頂点を利用すると鮮やかに多始点BFS問題をしばき倒すことができる感覚が確立されておらず、このままでは解説を読んで「なんて賢い手法なんだ」と感動したという記憶以外が残らない気しかしないのでまとめておく。
重みのないグラフについて、「特定の一頂点からの最短距離を全ての頂点に対して求めろ」と言われればさすがに幅優先探索で一撃だというのは感覚としても身に着いているが、本問における「加湿器が置かれている場所」のように、「始点となる条件を満たしている頂点が複数個存在する場合において、任意の頂点から最も近くにある始点までの距離を求めろ」と言われるとどう処理すればよいかよく分からず困る。そこで鍵となるのが超頂点(本来グラフには存在しないが、始点となり得る全ての頂点たちのみと辺で結ばれていると見なすことができる仮想的な頂点)を利用して特定の一頂点のみを始点とした幅優先探索解法に帰着させることである。
例として、以下の図1のようなグラフ(始点となるのは左側の楕円に囲まれた黄色い頂点たちであるとする)に対して本問と同様に「任意の頂点\(v\)について、\(v\)から見て最も近い位置にある始点\(s\)までの距離」を考える。
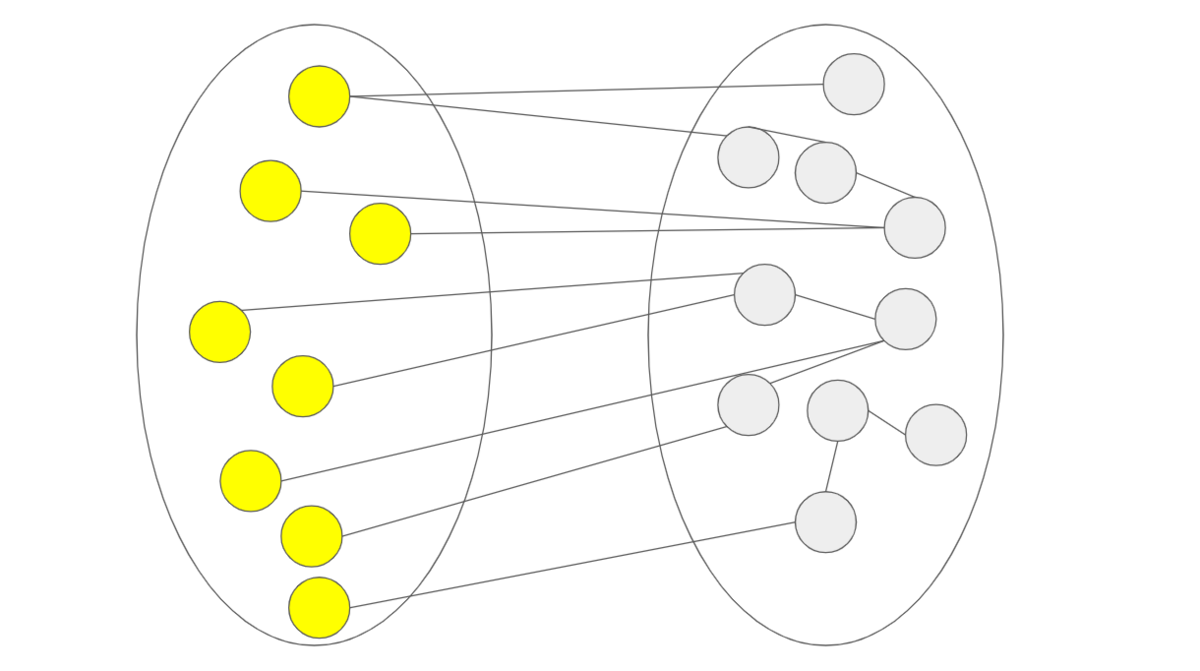
黄色い頂点を逐一キューに入れて単一始点の幅優先探索を行っても理論上答えは分かるが、頂点と辺の数が大きくなってくると圧倒的な効率の悪さを見せるためこのようなやり方を続けるという選択をすることはできない。そこで、以下図2のように、このグラフに対して超頂点(緑色で示す)を加え、それぞれの黄色い頂点と辺で直接つながっているものとする。

点線の辺も同じく重み無し(つまりは他の辺と同じく重さが\(1\)であると解釈できる)として扱うものとしておくと、緑色の超頂点のみをキューに入れていつものように幅優先探索を行うことにより、任意の頂点\(v\)について、(\(v\)から見て最も近くにある始点までの距離\(+1\))の値が分かるのである。幅優先探索を実行しきった後は、各頂点についての最短距離が比較対象となる基準値に\(1\)を足した値以下であるかを確認していけばよい。このようにすることで、始点となる頂点の数を\(N_s\)、グラフの頂点および辺の数をそれぞれ\(V, E\)とすると、一つ一つ始点をキューに入れて幅優先探索を繰り返すという愚直な方法にかかる\( \mathcal{O}(N_s (V + E) )\)から削減して、\( \mathcal{O}(V + E)\)の計算量で片付くようになるのである。
なお、ちょっと立ち止まって考えればすぐに分かることではあるのだが、実装上は本当に超頂点を用意して全ての始点たちと辺でつなぐという行為をする必要まではない。超頂点から始めた幅優先探索は、結局は超頂点をキューから取り出した直後のステップで全ての始点たちをキューに突っ込みながら最短距離の値を\(1\)と記録しているだけであるという点に着目すれば、じゃあそもそも最初から「全ての始点たちをキューに入れつつそれらについての最短距離を\(0\)と記録しておく」ことと決めておくのと等価であるため、本問の解説のように「最初に全ての始点たちをキューに突っ込み、最短距離を\(0\)と記録する」というように取り決めても全く問題ないと結論付けられる。同様の問題と出くわした際には是非とも自在に使いこなせるようにしておきたい。