↓問題のページ↓
500点が与えられているF問題ではあるが、自分でもある程度の方針が立つくらいには見た目ほどの難しさは持ち合わせていない一問。だからこそ直前の記事の通り、A問題でWAを被弾して動揺しまくったせいで十分な精度で考察できず本番でAC獲得しきれなかったのが途轍もなく悔しい。
※本番で忘れていたので残しておくメモ:グラフ理論における「次数」とは、注目している頂点から伸びている辺の数のことである
まず根本的な前提を確認していく。頂点\(u, v\)の間に新しく辺を追加すると、\(u, v\)それぞれの次数は\(1\)だけ大きくなるので、入力で与えられる木に対して新しく1辺を追加することによって出来上がる閉路を構成する全頂点の次数が\(3\)となるためには、\(u, v\)としてはどちらも次数が\(2\)の頂点を選ばなければならないと分かる。
次に、次数が\(2\)であるような2頂点の組のうち、どのようなものを選ぶのが適切なのかを考えよう。最も簡単な場合として、
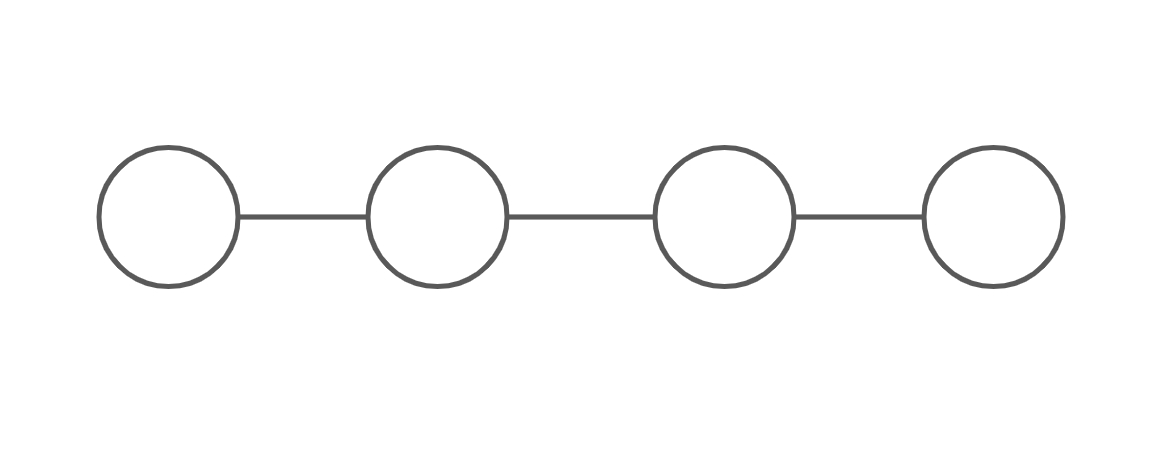
上図の木(というよりは直線グラフだがまあ木ではある)に対し、

このように1辺を追加する場合を考える。すると、構成する全頂点の次数が3であるような閉路が見事に出来上がる・・・のだが、これは明らかに多重辺を持つので「出来上がるグラフは単純グラフである」という条件を満たさない。というわけで、「互いに直接辺で結ばれた、次数が\(2\)であるような2頂点」を選ぶのはダメと分かる。それでは木がもう少し複雑化した場合を考えよう。

入力で与えられる木が上図のようである場合を考えてみる。次数が\(2\)である頂点は\(1,2,3,4,5\)の5つあるが、丁寧に見ていくと、適切な2頂点の選び方は\((1, 2), (2, 3), (3, 1)\)しかないと分かる(この3通り以外の選び方は次数が\(3\)でない頂点を閉路に含んでしまう、というのは以下の2つの図を見比べてみれば一目瞭然)。


このことから、次数が\(3\)であるような頂点と直接辺で結ばれている3頂点\(v_0, v_1, v_2\)のうち、ともに次数が\(2\)であるものを、追加で張る辺の2端点として選び出すもののみが適切な選び出し方であると分かる。
ここまでで、次数が\(3\)であるような頂点が1つしかない場合については、適切な2頂点の選び出し方が何通りあるかは簡単に求められると分かった。次数が\(3\)であるような頂点が2つ以上ある場合についても、それらが辺によって直接結ばれてはいなければ、それぞれの次数が\(3\)であるような頂点ごとに求めていけばよいことも分かる。残る問題は、「次数が\(3\)であるような頂点が2つ以上存在し、且つそれらが直接辺によって結ばれている場合」の処理である。それではまた別の図を使って考えていこう。

上図のような13頂点からなる木(次数が\(3\)である頂点2,5,6,10は赤枠に変えてある)について考えていく。これまでの話と同様に考えていくと、頂点2と辺で結ばれていて次数が\(2\)であるのは頂点1と3なので1通り、頂点5と辺で結ばれている頂点の中に次数が\(2\)であるものは存在しないので0通り、頂点6と辺で結ばれている頂点のうち次数が\(2\)であるのは7しかないので0通り、頂点10と辺で結ばれている頂点はどれも次数が\(2\)でないので0通り、よって合計1通りと言いたくなってしまうが、実際は以下2つの図のように、頂点1と7、頂点3と7を選んだ場合にも閉路を構成する全頂点の次数が\(3\)であるような単純グラフを構築することができるので正しく数え上げられていない。


ではどのようにすれば上手くいくかというと、互いに辺で結ばれており、次数が\(3\)であるような頂点たちを全て1つの頂点に併合してしまうのが良い。すなわち、もとの13頂点からなる木を以下のように変形してしまおう。

こうすることにより、次数が\(3\)であるような頂点が1つしかない場合についての問題に帰着することができる。
※念のため結果を確認しておくと、併合した頂点と辺で結ばれている頂点のうち、次数が\(2\)であるのは1,3,7の3つであるから、これらから異なる2つを選び出す方法は3通りある。というわけで、もとの状態から結果が変わらないことが分かった。
併合処理のやり方はきっといろいろあるのだろうが筆者は幅優先探索を選んだ。\(u = 0, 1, \dotsc , N - 1\)の順にそれぞれの頂点\(u\)を見ていき、次数が\(3\)であれば、\(u\)を始点とした幅優先探索を行い、辺で結ばれているそれぞれの頂点\(v\)が次数\(3\)ならばキューに入れ、\(3\)以外の次数ならば、キューの先頭と\(v\)間の辺を削除し、\((u, v)\)間に辺を張っていく。最後に、幅優先探索で見てきた頂点たちのうち\(u\)以外から伸びている辺を全て削除する。この処理が終わった後、\(u\)と辺で結ばれている頂点のうち、次数が\(2\)であるものの個数を数え上げ(この値を\(D\)とする)、\begin{align} \frac{D(D-1)}{2} \end{align}を答えに加算していくというようにした。このようにしてAC獲得。
計算量を雑に見積もると、頂点数\(N\)の木に対して何度か幅優先探索を行うことになるが、同じ頂点および辺を2度以上見ることはないため、探索対象となる頂点数の合計値は最悪でも確実に\(N\)以下であり、辺の数の合計値は確実に\(N - 1\)以下であるため\(\mathcal{O}(N)\)で実行可能である。